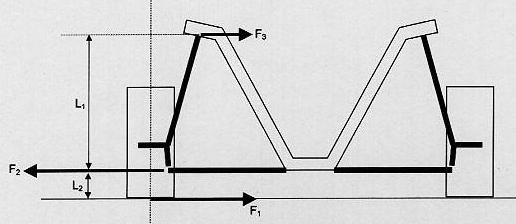
Here we have the forces of interest.  For this analysis only horizontal forces need be considered.  There are of course vertical forces, but during steady state cornering these cancel out and can be neglected.

We must begin by making some assumptions, using the earlier M3 as an example.  The weight and physics involved for the E46 3-series is effectively similar for comparative purposes   First, consider an M3 cornering such that it experiences 100% weight transfer at the front wheels.  This is not at all unusual on a modified M3.  We have probably all seen pictures of an M3 in a turn with its inside front wheel in the air.  That is a sure sign of 100% weight transfer.

Second, let us assume that our M3 is cornering at 1G.  Again, on a modified M3 with R-series tires, this is very plausible.  If an M3 weighs 2700 lbs and has close to a 50/50 weight distribution, then the outside front tire must generate a lateral force of 1350 lbs under the circumstances just outlined.  (an E36 M3 weighs approximately 3150 lbs. and also has a near 50/50 weight distribution)

Thus F1 = 1350 lbs as depicted in the figure above.  The figure is really a "free body diagram" which considers the forces that act ON the strut/wheel assembly.  These forces must sum to zero in the horizontal direction.  Also, the sum of the torque's acting on the strut/wheel assembly must cancel out.  Our goal is to determine the force F3 which is the force that the strut tower exerts on the strut assembly.  There is an equal and opposite force exerted on the strut tower BY the strut assembly.  (the comparable F1 for an E36 M3 is 1575 lbs.)

We can solve for F3 if we do a balance of torque's around the outer ball joint (where the control arm attaches to the strut).  What we get is:

F1(L2) = F3(L1)         or,         F3 = F1(L2/L1)

Now, we already know F1 = 1350 lbs.  And we can determine L1 and L2 from a quick measurement of an M3 (L1 = 24.3"  and  L2 =6.0").  Thus F3 = 333lbs.  (using the same L1 & L2 figures, the E36 M3 yeilds an F3 of 389 lbs.)

So the conclusion is that when an M3 corners at 1G with 100% weight transfer at the front wheels, there is a 333 lb force pulling OUT on the outer strut tower.  Since the inside wheel is un-loaded there is no corresponding force generated at the inside strut tower.  Therefore a strut tower bar tends to be in tension, not compression as is often believed.

Now we ask ourselves: How critical is a force of 333 lbs pulling on the outer strut tower?

This 333 lb load amounts to about 12% of the car's total weight.  Even though the strut tower is designed mainly to manage vertical forces, 333 lbs in the horizontal direction is not going to permanently deform the chassis.  But the problem is that this force is repeatedly applied over many cycles during the life of the car.  The more you drive it hard the more cycles you generate.  This can lead to fatigue failure of the material that forms the strut tower (or where the strut tower attaches to the inner fender well).

What a strut bar does is tie the two strut towers together so that they share the load applied at the outer tower.  This gives you twice as much material to deal with the same cornering force and helps reduce fatigue stress in this area.

Another point to consider is that if your outer strut tower is deflected outwards 0.20" by this 333 lb force, then you just lost 0.5° of negative camber!  If it deflects 0.42" you have lost a full degree of negative camber.